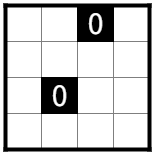
盤面のヒントマスを黒マスや白マスに置換しても正解の照明(解)の位置が変わらないことがある。
このとき、ヒントマスが置換された後の盤面を根盤面(コンバンメン)と呼ぶ。
その逆を葉盤面(ヨウバンメン)と呼ぶ。
根盤面は、冗長性が省かれた盤面と言い換えられる。
冗長性を省いた盤面がそうでない盤面よりも必ずしも良い問題になるとは限らない。

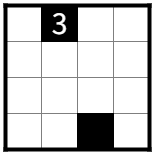
たとえば、図1-1の解はR1C1、R2C4、R4C3になる。
※"RnCm"とは左上から数えてn行目、m列目のマスのこと。"(n,m)"表記よりもタイプ数が少ない。"n:m"などにするともっと少なくなるがこちらは慣例が無い。
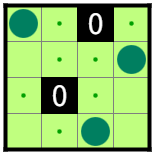
図1-2のR3C4に1を追加しても解は変わらない。
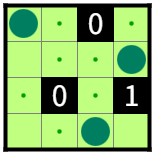
図1-2のR4C1に0を追加しても解は変わらない。
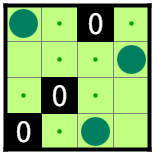
図1-2のR4C4に1を追加しても解は変わらない。
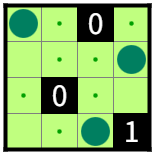
図1-2のR3C4に1を、R4C1に0を、R4C4に1を同時に追加しても解は変わらない。
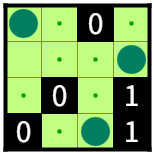
このとき、図1-2を図1-2-1、図1-2-2、図1-2-3、図1-2-4の根盤面と呼ぶ。
また、図1-2-1、図1-2-2、図1-2-3はそれぞれ図1-2-4の根盤面でもある。
このように、根盤面と葉盤面の対応は一対多になることも、多対一になることもある。
ヒントマスを黒マスにのみ置き換えた根盤面を特に黒-根盤面と呼ぶ。
ヒントマスを白マスにのみ置き換えた根盤面を特に白-根盤面と呼ぶ。
ヒントマスを白マスと黒マスの両方に置き換えた根盤面を特に白黒-根盤面と呼ぶ。
これらは思考のタネとして定義した概念で、現時点でこの概念を使って推論を展開することはない。
照明の位置の決まり方には順番がある。
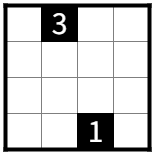
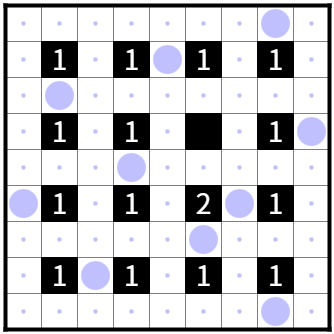
たとえば、図2-1の解はR1C1、R1C3、R2C2、R4C4である。
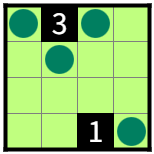
これらの解は、R1C1=R1C3=R2C2→R4C4という順で決まっている。
R1C1、R1C3、R2C2が決定するとR4C4が決定されるが、R4C4が決定されてもR1C1、R1C3、R2C2が決定されないからだ。
このように美術館の解には順序がある。
解に順序がある場合、盤面を次のように分離して考えることができる。

根盤面の関係に似ているが、図2-2-1と図2-1、図2-2-2と図2-1はそれぞれ解が異なるので、根盤面には当てはまらない。
図2-2-1の解が図2-2-2の解を支配している(図2-2-2の解が図2-2-1の解に従属している)ことが分かれば、図2-1を解く問題は、図2-2-1を解いて図2-2-2を解く問題に帰着できる。
解同士のこのような関係が分かれば、その関係を樹形図で表すことができるようになるだろう。
ただし確定順がどのように決定されるかは今ところ不明。
確定順が一意に定まるかどうかも分かっていない。
さらなる探求が必要だ。
ある盤面のヒントマスをすべて黒マスに置換する。
このとき、解の条件を満たす照明の個数の最大値・最小値はいくらになるか?
ph.氏がnoteで取り上げている考え方だ。

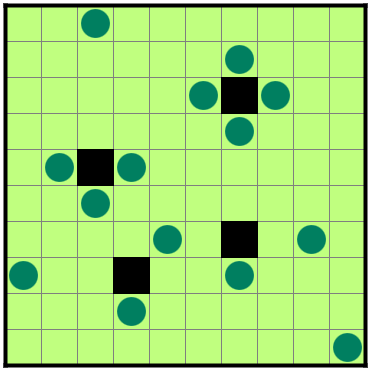
たとえば、図3-1のときは、最大で14個、最小で10個になる。
理論上の最大値は、黒マスが分割する列(以下、分割列)の数と、黒マスが分割する行(以下、分割行)の数の小さい方だ。
図3-1は分割行数=分割列数=14だから、理論最大値は14だ。
理論上の最小値は、盤面の列数と盤面の行数=10の小さい方だ。
図3-1の盤面の列数=行数=10だから、理論最小値は10だ。
ただし、個数は必ずしも理論値と等しくなるわけではない。

たとえば、図3-2の盤面(出典)の最大個数は58である。

分割行数=分割列数=61なので、理論上は61個。
にもかかわらず、実際には58個が限界だ。
幅1の行が潰し合い、3個分の照明が置けなくなっているからだ。
また、22×22の盤面だが、照明22個では充填できそうにない。(現在見つかっている最小照明数は32。)

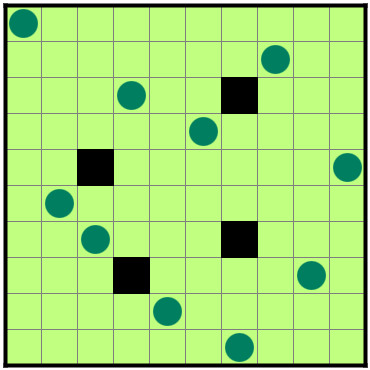
図3-3の盤面(出典)は、最大値は理論値と一致する。


現在見つかっている最小照明数は20だが、最小かどうかは分からない。

最大照明数と最小照明数が分かれば挟み込みで解ける問題も出てくるだろう。
だがもしそれらを求めるのに問題を解くのと同じだけの計算量が必要になるならば意義は小さい。
さらなる探求が必要だ。
以下は、難易度のさまざまな捉え方をまとめたもの。
以下の配置を使ってリアルタイムソルバーを使いながらヒント数字を調整すると簡単に複雑な問題が作れる。


配置パターン数:1
縦横の長さが奇数(かつ5以上)のときのみ成立。
部分解の積み重ねが全体解にならないことが多い。
カウンティングを使って解けることがある。


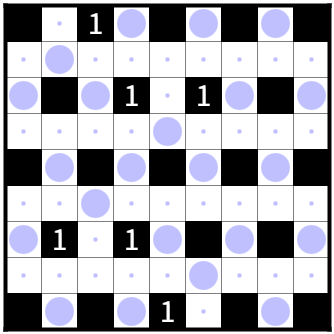
配置パターン数:8(粗密方向(縦or横)が2パターン、横方向に2パターン、縦方向に2パターン)
部分的に手筋が発生するので積み重ねで解けることが多い。


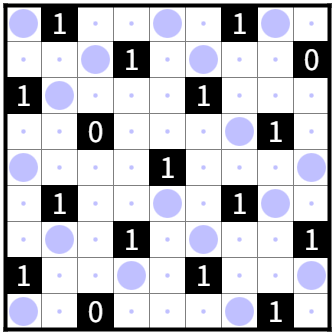
配置パターン数:10(傾きが2パターン、縦横方向に5パターン)
縦横の長さが5以上のときのみ成立。(4以下で無理やり定義できないこともない。)
手筋がほとんど通用しない。ただし部分解の積み重ねが全体解に繋がることが多い。
確認レベルとは、照明を置く前にその位置が正しいかどうかをどれだけ確認するかの度合。
どの前提を認めないかによって論理的に分類できる。
主にDaily Akariのプロモードで正確性を高めるときに問題になる。
確認レベルを上げることは縛りプレイとも言えるが、それによって試行錯誤では気付けない深い構造に気づくこともある。
最終更新日: 2026-01-24
© 2026 T.Y.